Line transect census of Hazel Grouse (Tetrastes bonasia). Determination of observational correction coefficients in different time of breeding season.
Pyytä on pidetty kanahaukan perusruokavalioon kuuluvana saaliseläimenä.
Tosin viime vuosina useimmin kanahaukan pesiltä on löytynyt rastaiden ja
varislintujen saalisjätteitä. Tästä huolimatta tai ehkä juuri sen takia olen
ottanut tavakseni, petolintuseurantojen yhteydessä, selvittää pyiden
vuosittaiset tiheydet linjalaskennoilla. Laskenta on pääosin suoritettu
kuusivaltaisilla mustikkatyypin biotoopeilla. Laskentakilometrit ovat vaihdelleet vuosittain 140-340 km välillä.
Olen käyttänyt yksikkönä paria/km2. Pariksi on tulkittu:
yksittäinen lintu, 2 lintua (pariutuneet), poikue. RKTL ilmoittaa tiheydet
syksyisin yksilöä/km2, jossa myös poikaset laskettu lukumäärään mukaan.
Tulokset eivät siis ole suoraan keskenään vertailukelpoisia.
Linjalaskennassa erotetaan 25+25m pääsarka (MB) ja sen
ulkopuolinen apusarka. Yhdessä niitä kutsutaan tutkimussaraksi (SB). Laskennat
on yleensä suoritettu aamupäivisin klo 04:00 – 12:00 välisenä aikana. Jotta havaintoja
saataisiin riittävästi, olen suorittanut laskennat huhti-heinäkuun aikana. Eri
kuukausien havainnot on käsitelty erikseen, koska pyyn havaittavuus on
huomattavan erilainen pesimäkauden eri vaiheissa. Huhti-toukokuussa pyykoiraat
viheltelevät innokkaasti ja havaittavuus on hyvä muutoin vielä melko
hiljaisissa metsissä. Normaaliin linjalaskenta-aikaan kesäkuussa havaittavuus
on heikoin. Naaraat makaavat tiukasti pesillään eivätkä koiraat enää vihellä.
Voi helposti kävellä yli 50 km MT-kuusikossa ilman yhtään pyyhavaintoa. Heinäkuussa havaittavuus taas paranee
poikueiden myötä.
Teoriassahan parimäärä pitäisi huhti-heinäkuussa olla melko
suora tai (kuolevuuden takia) loivasti laskeva käyrä, eikä pomppia ylös-alas.
Tietysti tarkalleen samaa tiheyttä saman vuoden eri kuukausina ei odoteta,
koska ei tutkita joka kuukausi samaa neliötä, vaan tutkimusalueen eri kolkkia.
Ennen kuukausittaisten korjauskerrointen määrittämistä,
halusin korjata vuosittaista vaihtelua. Eri vuosina pyykanta vaihtelee ja tämä
näkyy tietysti myös kuukausikohtaisissa havainnoissa. Tämän tein seuraavasti:
Määritin ensin havaintokeskiarvon kullekin vuodelle (2010 - 2014) erikseen (Xv). Vuosittaisista keskiarvoista
otettiin edelleen keskiarvo (Xvn).
Kuukauden korjattu tiheys linjakilometriä kohti (N’k) saatiin tällöin kaavasta (1):
missä Nk on
korjaamaton linjatiheys tietyn vuoden tietyssä kuussa.
Tämän jälkeen päästiin määrittämään kuukausikohtaiset
korjauskertoimet. Päälaskentakuukaudelle eli toukokuulle annettiin arvo 1.0 ja
muiden kuukausien korjaukset laskettiin vertaamalla toukokuun (2010-2014) keskiarvotiheyteen.
Oletuksena oli, että laskentareitit valikoituivat vuosittain satunnaisesti eri
kuukausille. Kuten taulukosta 1 nähdään, huhtikuussa havaittavuus oli keskimäärin
1.5-kertaa suurempi kuin toukokuussa. Kesäkuussa havaittavuus oli alle 30 %
toukokuun arvosta.
 |
| Tbl1. Montly (Apr-Jul) observations / line km of grouse in 2010-2014 and thus formed observability indices |
R. A. Väisänen on laskenut kuuluvuuskertoimen (K) alla
olevasta kaavasta:
 |
| Eq.2. Calculation of correction coefficient for line transect censuses by R.A. Väisänen |
missä p tarkoitta
pääsarkahavaintojen osuutta kaikista havainnoista.
Enää en muista, mistä todennäköisyysfunktioavaruudesta Väisänen otti tuon neliöjuurtamisen, mutta oikeaa tulosta se ei anna. Oikea parimäärä
vähäisillä apusarkahavainnoilla saadaan yksinkertaisesti:
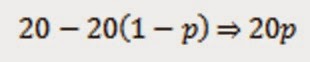 |
| Eq.3. Calculation of correction coefficient for line transect censuses by T.O. Niemi |
Problematiikkaa on havainnollistettu alla olevassa
kaaviossa:
 |
| Diag1. Comparison of correction coefficients and densities Väisänen (K,km)/Niemi (K',km') with different SB-observation numbers when MB-obeservations are set to 1. |
Kaaviossa pääsaralla havaitaan yksi yksilö jokaista
kilometriä kohti, mutta tutkimussarkahavainnot/km, jotka esitetty x-akselilla
kasvavat oikealle. K-kertoimet (K=Väisänen, K’=Niemi) lähenee nollaa
tutkimussarkahavaintojen kasvaessa, mutta parimäärä pitäisi olla koko ajan 20.
Nähdään että juurrettu funktio ylikorostaa parimäärää lajeilla, joilla pääosa
havainnoista tulee pääsaralta.
Väisänen on jostain aineistosta laskenut p-suhteeksi 0.629 (K= 15.63). Minä
laskin tämän kevään aineistosta 0.667 (K’= 13.34), jota olen käyttänyt tässä
tarkastelussa.
Koska pääsarankin linnuista osa jää havaitsematta, on
lisäksi laskettu yleinen korjauskerroin, jonka arvoksi saatiin 0.76. Näiden
kertoimien jälkeen päästää muodostamaan pyyn kuukausikohtaiset parimäärät ja
edeleen vuosikohtainen parimäärä.
| Eq4. Calculation of density |
Pyyn laskettu tiheys linjalaskennoissa 2010 – 2014 on
esitetty taulukossa 2.
 |
| Tbl2. Calculated densities of Hazel Grouse in Northern Satakunta, years 2010-2014 |
Satunnaisvaihtelun sallimissa rajoissa usein tyydytään vertailemaan
vain runsausindekseillä. Eli selvitetään sitä, miten populaatiotieheys
vaihtelee vuosittain. Kaaviossa 2 on esitetty pyyn tiheys tutkimusalueella vuosina 2008-2014. Vuoden 2008 arvoksi on asetettu 100.
 |
| Diag.2. Relative abundance of Hazel Grouse. Years 2008-2014. Value of 2008 is set to 1. |
Linjalaskentametodi ei luonnollisesti ole absoluuttinen.
Verrattuna todellisiin tiheyksiin, virhettä aiheuttaa normaali otoksen
määrittämiseen liittyvä problematiikka, satunnaisvaihtelut mm. havaittavuudessa
ja käytetty kuuluvuuskerroin. Itse olisin taipuvainen suosittelemaan pelkän
pääsarka-aineiston käyttämistä lajeilla, joilla pääsarkahavaintojen osuus on
suuri.

